老王的夢田

1999年第35屆蒙古數學奧林匹克第九級第三題

【題目】

設M為三角形ABC的重心，並假設直線AB與三角形AMC的外接圓相切。證明：
sin(∠CAM) + sin(∠CBM) ≦ 2/√3。

【證明】

如圖，

假設D、E、F分別是邊BC、AC和AB的中點，∠CAM＝θ，∠CBM＝φ

因為FA是圓AMC的切線，所以

∠FAM＝∠ACM

且FA²＝FM×FC

又FA＝FB，故FB²＝FM×FC

知道FB是三角形BMC的切線

∠FCM＝∠BCM

再令∠FAM＝∠ACM＝α，∠FCM＝∠BCM＝β。

作三角形ABC的外接圓，並延長AM交圓於另一點H，如圖，

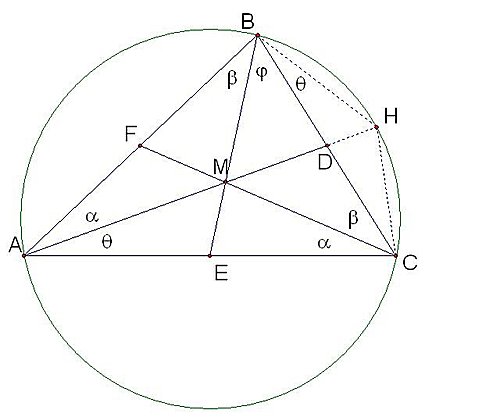
∠BHM＝∠BCA＝α＋β＝∠BMH，

故BM＝BH

整理FB²＝FM×FC可得

FB²＝(FC/3)×FC＝FC²/3

所以FB：FC＝1：√3

又可以得道△FBM ~△FCB

BM：BC＝FB：FC，而BC＝2BD故

BM：BD＝2：√3

最後由張角定理（註），在三角形BMH中

(sinθ)/BM＋(sinφ)/BH＝(sin(θ＋φ))/BD

sinθ＋sinφ＝(BM/BD)×sin(θ＋φ)＝(2/√3)×sin(θ＋φ)

由於sin(θ＋φ)≦1，故得證

sinθ＋sinφ ≦ 2/√3

【註】

張角定理：在三角形ABC中，D在BC邊上，那麼有：

sin(∠BAD)/AC＋sin(∠CAD)/AB＝sin(∠BAC)/AD。

證明只要用面積就可以。

(ABD)＋(ACD)＝(ABC)

(1/2)×AB×AD×sin(∠BAD)＋(1/2)×AC×AD×sin(∠CAD)＝(1/2)×AB×AC×sin(∠BAC)

同乘上2，再同除以AB×AC×AD就得到定理的結果。